Bộ đề thi học kì 1 môn Toán lớp 9 năm 2022

[ad_1]

Nội dung đang xem: Bộ đề thi học kì 1 môn Toán lớp 9 năm 2022 – 2023

Đề thi cuối kì 1 Toán 9 năm 2022 – 2023 tuyển chọn 8 đề kiểm tra cuối kì 1 có đáp án chi tiết và bảng ma trận đề thi.

Đề thi học kì 1 Toán 9 được biên soạn với cấu trúc đề rất đa dạng cả trắc nghiệm, tự luận kèm theo và cả đề 100% tự luận, bám sát nội dung chương trình học trong sách giáo khoa Toán 9 tập 1. Hi vọng đây sẽ là tài liệu hữu ích cho quý thầy cô và các em ôn tập và củng cố kiến thức, chuẩn bị sẵn sàng cho học kì 1 lớp 9 sắp tới. Vậy sau đây là nội dung chi tiết TOP 8 đề thi cuối kì 1 Toán 9 năm 2022 – 2023, mời các bạn cùng theo dõi tại đây.

Danh Mục Bài Viết

Bộ đề thi học kì 1 Toán 9 năm 2022 – 2023 có đáp án

Đề thi học kì 1 Toán 9 – Đề 1

Đề thi học kì 1 Toán 9

I. PHẦN TRẮC NGHIỆM : (3 điểm )

Khoanh tròn vào chữ cái ở đầu câu với những câu trả lời đúng (mỗi câu đúng 0,25 điểm)

Câu 1. Với những giá trị nào của x thì $sqrt{x - 2020}$ có nghĩa

A. x > 2020

B. x > -2020

C. x ≥ 2020

D. x ≤ 2020

Câu 2. Căn bậc hai số học của 9 là:

A. 81

B . 3

C. 81

D . 3

Câu 3. Đồ thị hàm số y = 2x -3 đi qua điểm nào?

A. (1; -3)

B. (1; -5)

C. (-1; -5)

D. (-1; -1)

Câu 4. Hàm số y= (m – 5)x + 2 là hàm số đồng biến khi nào?

A. m <5

B. m >5

C. m <-5

D. m >-5

Câu 5. Để hàm số y = (m +1)x -3 là hàm số bậc nhất thì:

A. $m neq-1$

B. $m neq 1$

C. m=-1

D. m=1

Câu 6. Cho hàm số bậc nhất $mathrm{y}=(mathrm{m}-3) mathrm{x}-4 và mathrm{y}=4 mathrm{x}$ . Giá trị của m đề đồ thị của hai hàm số cắt nhau là:

A. $m neq 3$

B. $m neq 7$

C. $m neq-3, m neq-7$

D. $m neq 3, m neq 7$

Câu 7. Tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm, AC = 8cm. Độ dài AH là:

A. 3,5cm

B. 4,6cm

C. 4,8cm

D. 5cm

Câu 8. Cho tam giác ABC vuông tại B. Khi đó SinC bằng:

$A. frac{A B}{A C}$

$B. frac{A C}{A B}$

$C. frac{B C}{A C}$

$D. frac{A B}{B C}$

Câu 9. Đường thẳng và đường tròn tiếp cắt nhau thì số điểm chung là:

A. 0

B. 1

C. 2

D. 3

Câu 10. Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường nào?

A. Phân giác

B. Trung tuyến

C. Đường cao

D. Trung trực

Câu 11. Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm ở vị trí nào?

A. Nằm ngoài đường tròn

B. Nằm trên đường nối tâm

C. Nằm ngoài đường nối tâm

D. Nằm trong đường tròn

Câu 12. Nếu AB là một dây bất kì của đường tròn (O; R) thì:

$A. A B leq 2 R$

$B. A B<2 R$

C. AB>2 R

$D. A B leq R$

II/ PHẦN TỰ LUẬN : (7 điểm)

Bài 1. (1,5 điểm).

a) Tính $M=-sqrt{18}+sqrt{32}+2019 sqrt{2}$

b) Rút gọn biểu thức $N=left(frac{sqrt{x}}{sqrt{x}+1}+frac{sqrt{x}}{sqrt{x}-1}right): frac{2}{x-1} quad$ (với $mathrm{x}>0$ và $mathrm{x} neq 1$ )

Xem thêm: Tuyển tập 95 đề thi vào lớp 10 của các sở trên cả nước hệ không chuyên

Bài 2. (1,5 điểm) Cho hàm số y=(m-1) x+m+4

a) Vẽ đồ thị hàm số trên với m = -1.

b) Tìm m để đồ thị hàm số (1) song song với đồ thị hàm số y = -x + 2.

Bài 3. (3 điểm) Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm A, bán kính AH, kẻ các tiếp tuyến BD, CE với đường tròn tâm A (D, E là các tiếp điểm khác H). Chứng minh rằng:

a) Ba điểm D, A, E thẳng hàng;

b) DE tiếp xúc với đường tròn có đường kính BC.

Bài 4. (1 điểm) Giải phương trình:

$sqrt{x- 2 }- 3sqrt{x ^2- 4 }= 0$

Đáp án đề thi học kì 1 Toán 9

I.TRẮC NGHIỆM: ( 3 điểm )

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	C	B	C	B	A	D	C	A	C	D	B	A

Mỗi câu trả lời đúng 0,25đ

II.TỰ LUẬN ( 7 điểm )

Bài

Nội dung – Đáp án

Điểm

$begin{aligned} & text { a) } M=-sqrt{18}+sqrt{32}+2019 sqrt{2} =&-3 sqrt{2}+4 sqrt{2}+2019 sqrt{2} =& 2020 sqrt{2} text { b) } & N=left(frac{sqrt{x}}{sqrt{x}+1}+frac{sqrt{x}}{sqrt{x}-1}right): frac{2}{x-1} =& frac{sqrt{x} cdot(sqrt{x}-1)+sqrt{x} cdot(sqrt{x}+1)}{(sqrt{x}+1) cdot(sqrt{x}-1)}: frac{2}{x-1} =& frac{2 x}{x-1}: frac{2}{x-1}=frac{2 x}{x-1} cdot frac{x-1}{2}=x end{aligned}$

0,5đ

………….

Ma trận đề thi học kì 1 Toán 9

Chủ đề	Nhận biết		Thông hiểu		Vận dụng				Tổng
					Vận dụng thấp		Vận dụng cao
	TN	TL	TN	TL	TN	TL	TN	TL
1. Căn bậc hai	Biết được đk để căn thức có nghĩa, căn bậc hai của số không âm		Hiểu được căn bậc hai số học		Sử dụng phép bđ đưa thừa số ra ngoài dấu căn. Sử dụng các phép biến đổi để thu gọn biểu thức chứa căn bậc hai		Giải phương trình chứa căn bậc hai
Số câu Số điểm Tỉ lệ	1 0,25 2,5%		1 0,25 2,5%			2 1,5 15%		1 1 10%	5 3 30%
2. Hàm số	Nhận biết được hàm số đồng biến, hàm số bậc nhất		Xác định được điểm thuộc đồ thị hàm số		Tìm đk để đường thẳng cắt nhau, song song. Vẽ được đồ thị hàm số bậc nhất
Số câu Số điểm Tỉ lệ	2 0,5 5%		1 0,25 2,5%		1 0,25 2,5%	2 1,5 15%			6 2,5 25%
3. Một số hệ thức về cạnh và đường cao. Tỉ số lượng giác	Nhận biết được tỉ số lượng giác của góc nhọn		Hiểu được hệ thức để tính độ dài đường cao
Số câu Số điểm Tỉ lệ	1 0,25 2,5%		1 0,25 2,5%						2 0,5 5%
4. Đường tròn	Biết được số điểm chung của đường thẳng và đường tròn. Liên hệ giữa đường kính và dây		Hiểu được tính chất của đường nối tâm. Tâm đường tròn ngoại tiếp tam giác		Chứng minh được 3 điểm thẳng hàng và một đường thẳng là tiếp tuyến của đường tròn
Số câu Số điểm Tỉ lệ	2 0,5 5%		2 0,5 5%			2 3 30%			6 4 40%
Tổng số câu Tổng số điểm Tỉ lệ	6 1,5 15%		5 1,25 12,5%		1 0,25 2,5%	6 6 60%		1 1 10%	19 10 100%

………….

Đề thi cuối kì 1 Toán 9 – Đề 2

Đề thi học kì 1 Toán 9

Câu 1: Thực hiện các phép tính:

a) $sqrt{12}+5sqrt{3}-sqrt{48}+sqrt{75}$

b) $sqrt{{{left( 1-2sqrt{5} right)}^{2}}}+sqrt{{{left( sqrt{45}+1 right)}^{2}}}$

Câu 2: Giải phương trình:

a) $sqrt{3x-1}=sqrt{5}$

b . $sqrt{{{x}^{2}}-6x+9}=9$

c. $sqrt{{{x}^{2}}+8x-5}=x-1$

Câu 3: Cho biểu thức

$A=left( frac{1}{sqrt{x}-1}-frac{1}{sqrt{x}} right):left( frac{sqrt{x}+1}{sqrt{x}-2}-frac{sqrt{x}+2}{sqrt{x}-1} right)$

a. Tìm điều kiện của x để biểu thức A có nghĩa.

b. Rút gọn biểu thức A

c. Tìm giá trị của x để A = 1/6

Câu 4: Cho hàm số bậc nhất y = (m + 5) + 2m – 10y

a. Với giá trị nào của m thì hàm số nghịch biến.

b. Tìm giá trị của m để đồ thi cắt trục tung tại điểm có tung độ bằng 9.

Bài 5: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh CB thành hai đoạn CH = 8, BH = 3. Gọi M, N lần lượt là chân các đường vuông góc hạ từ H xuống AB và AC.

a. Tính độ dài MN.

Xem thêm: Tài liệu ôn thi cấp tốc Đại số lớp 9

b. Chứng minh rằng: AN . AC = AM . AB

c. Chứng minh MN là tiếp tuyến của đường tròn đường kính OO’, biết O, O’ lần lượt là tâm đường tròn ngoại tiếp tam giác BHM, NHC.

Câu 6: Cho a, b, c là các số thực dương thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức: $M=frac{1}{a+b+1}+frac{1}{b+c+1}+frac{1}{c+a+1}$

Câu 1:

a. $sqrt{12}+5sqrt{3}-sqrt{48}+sqrt{75}=2sqrt{3}+5sqrt{3}-4sqrt{3}+5sqrt{3}=8sqrt{3}$

b. $sqrt{{{left( 1-2sqrt{5} right)}^{2}}}+sqrt{{{left( sqrt{45}+1 right)}^{2}}}=left| 1-2sqrt{5} right|+left| 3sqrt{5}+1 right|=2sqrt{5}-1+3sqrt{5}+1=5sqrt{5}$

Câu 2:

a. $sqrt{3x-1}=sqrt{5}$

Điều kiện: $xge frac{1}{3}$

$sqrt{3x-1}=sqrt{5}$ <=> 3x – 1 = 5 <=> x = 2 (thỏa mãn)

Vậy phương trình có nghiệm x = 2

b. $sqrt{{{x}^{2}}-6x+9}=9$

Điều kiện: x² – 6x + 9 = (x – 3)² ≥ 0 ∀x

$begin{align} & ptLeftrightarrow sqrt{{{left( x-3 right)}^{2}}}={{3}^{2}}Leftrightarrow left| x-3 right|=3 & Leftrightarrow left[ begin{matrix} x-3=3 x-3=-3 end{matrix}Leftrightarrow left[ begin{matrix} x=6 x=0 end{matrix} right. right. end{align}$

Vậy phương trình có nghiệm x = 0 hoặc x = 6

c. $sqrt{{{x}^{2}}+8x-5}=x-1$

Điều kiện: ${{x}^{2}}+8x-5ge 0$

PTTĐ $Leftrightarrow left{ begin{matrix} x-1ge 0 {{left( sqrt{{{x}^{2}}+8x-5} right)}^{2}}={{left( x-1 right)}^{2}} end{matrix}Leftrightarrow left{ begin{matrix} xge 1 {{x}^{2}}+8x-5={{x}^{2}}-2x+1 end{matrix} right. right.Leftrightarrow left{ begin{matrix} xge 1 x=dfrac{3}{5}left( L right) end{matrix} right.$

Vậy phương trình vô nghiệm.

Câu 3:

$A = left( {frac{1}{{sqrt x - 1}} - frac{1}{{sqrt x }}} right):left( {frac{{sqrt x + 1}}{{sqrt x - 2}} - frac{{sqrt x + 2}}{{sqrt x - 1}}} right)$

a) Điều kiện $x geqslant 0,x ne 4,x ne 1$

$begin{matrix} A = dfrac{{sqrt x - sqrt x + 1}}{{sqrt x left( {sqrt x - 1} right)}}:left[ {dfrac{{left( {sqrt x + 1} right)left( {sqrt x - 1} right)}}{{left( {sqrt x - 2} right)left( {sqrt x - 1} right)}} - dfrac{{left( {sqrt x + 2} right)left( {sqrt x - 2} right)}}{{left( {sqrt x - 2} right)left( {sqrt x - 1} right)}}} right] hfill A = dfrac{1}{{sqrt x left( {sqrt x - 1} right)}}:dfrac{{x - 1 - left( {x - 4} right)}}{{left( {sqrt x - 2} right)left( {sqrt x - 1} right)}} hfill A = dfrac{1}{{sqrt x left( {sqrt x - 1} right)}}.dfrac{{left( {sqrt x - 2} right)left( {sqrt x - 1} right)}}{3} hfill A = dfrac{{sqrt x - 2}}{{3sqrt x }} hfill end{matrix}$

c) $A = frac{1}{6} Leftrightarrow frac{{sqrt x - 2}}{{3sqrt x }} = frac{1}{6} Leftrightarrow 2sqrt x - 4 = sqrt x Leftrightarrow sqrt x = 4 Leftrightarrow x = 16$

Vậy A = $frac{1}{6}$ khi và chỉ khi x = 16

Câu 5:

bo de thi hoc ki 1 mon toan lop 9 nam 2022 2023 1

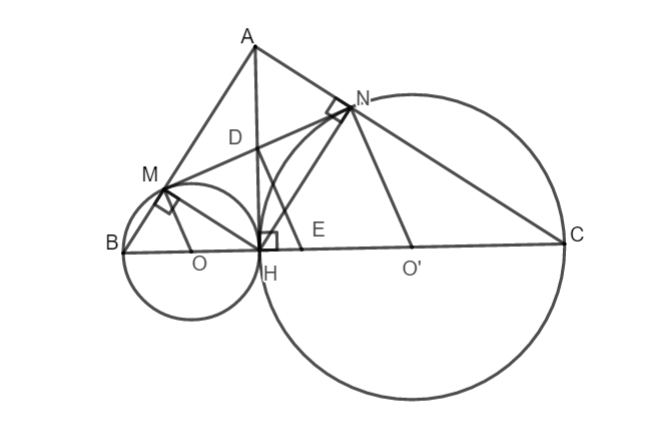
a) Ta có: $widehat {HMA} = widehat {ANH} = widehat {MHN} = {90^0} Rightarrow$ AMHN là hình chữ nhật

$Rightarrow MN = AH = sqrt {BH.HC} = sqrt {24} = 2sqrt 6$

b) AN . AC = AM . AB (cùng bằng AH²)

c) Ta có tam giác MHB vuông tại M nên O là trung điểm của BH.

Tương tự với tam giác NHC vuông tại N nên O’ là trung điểm của CH.

Gọi D là giao điểm của MN và AH, E là trung điểm của OO’

Ta có:

$widehat {MNH} + widehat {HNO'} = widehat {DNH} + widehat {HNO'} = {90^0} Rightarrow MN bot NO'$

$widehat {OMH} + widehat {HMD} = widehat {OHM} + widehat {MHD} = {90^0} Rightarrow MN bot OM$

Vậy tam giác ODO’ vuông tại D, D thuộc đường tròn đường kính OO’

Lại có ED là đường trung bình của hình thang OMNO’ $Rightarrow ED bot MN$

Vậy MN là tiếp tuyến của đường tròn đường kính OO’

Câu 6:

Với a, b, c là các số dương thảo mãn abc = 1 ta đặt $a = {x^3},b = {y^3},c = {z^3} Rightarrow xyz = 1$

Ta có:

$a + b + 1 = {x^3} + {y^3} + xyz = left( {x + y} right)left( {{x^2} - xy + {y^2}} right) + xyz geqslant left( {x + y} right).xy + xyz = xyleft( {x + y + z} right)$

Tương tự ta có:

$begin{matrix} b + c + 1 = {y^3} + {z^3} + xyz = left( {y + z} right)left( {{y^2} - yz + {z^2}} right) + xyz geqslant left( {y + z} right).yz + xyz = yzleft( {x + y + z} right) hfill c + a + 1 = {z^3} + {x^3} + xyz = left( {z + x} right)left( {{z^2} - zx + {x^2}} right) + xyz geqslant left( {z + x} right).zx + xyz = zxleft( {x + y + z} right) hfill Rightarrow M = dfrac{1}{{a + b + 1}} + dfrac{1}{{b + c + 1}} + dfrac{1}{{c + a + 1}} leqslant dfrac{{xyz}}{{xyleft( {x + y + z} right)}} + dfrac{{xyz}}{{yzleft( {x + y + z} right)}} + dfrac{{xyz}}{{zxleft( {x + y + z} right)}} = 1 hfill end{matrix}$

Suy ra GTNN của Q bằng 1 khi và chỉ khi x = y = z = 1 hay a = b = c = 1

Ma trận đề thi học kì 1 Toán 9

Cấp độ Chủ đề	Nhận biết	Thông hiểu	Vận dụng		Cộng
	Nhận biết	Thông hiểu	*Cấp độ thấp*	*Cấp độ cao*
	TL	TL	TL	TL
1.Căn thức bậc hai	– Xác định điều kiện có nghĩa của căn bậc hai.	-Hiểu được hằng đẳng thức để rút gọn biểu thức	Vận dụng các phép biến đổi đơn giản để rút gọn biểu thức, tính giá trị biểu thức	Vận dụng các phép biến đổi để rút gọn biểu thức phức tạp, giải phương trình vô tỷ
1.Căn thức bậc hai	Số câu:2 Số điểm:1	Số câu:2 Số điểm:1	Số câu:2 Số điểm: 1.	Số câu:1 Số điểm:0,5	*Số câu: 7* *Số điểm:3.5*
2.Hàm số bậc nhất	Nhận biết được hàm số đồng biến, nghich biến	Hiểu được hai đường thẳng song song,.. Vẽ được đồ thị hàm số	Tìm được giao điểm đồ thị của hai hàm số bậc nhất
2.Hàm số bậc nhất	Số câu:2 Số điểm:1	Số câu:2 Số điểm:1	Số câu:2 Số điểm:1		*Số câu: 6* *Số điểm: 3*
3.Hệ thức lượng trong tam giác vuông.		Hiểu được các hệ thức áp dụng vào tam giác vuông	Vận dụng các hệ thức lượng trong tam giác vuông để giải toán
3.Hệ thức lượng trong tam giác vuông.		Số câu:1 Số điểm:0.5	Số câu:1 Số điểm:0.5		*Số câu: 2* *Số điểm:* *1.0*
4. Đường tròn	Nhận biết được đường tròn	Hiểu được tính chất đường tròn, hai tiếp tuyến cắt nhau để chứng minh	Vận dụng khái niệm đường tròn và các tính chất đường tròn, hai tiếp tuyến cắt nhau của đường tròn để chứng minh
4. Đường tròn	Số câu:1 Số điểm: 05	Số câu:1 Sốđiểm:0.5	Số câu:2 Số điểm 1	Số câu:1 Số điểm:0.5	*Số câu: 5* *Số điểm:3*
*Tổng*	Số câu:4 Số điểm: 2.0	Số câu: 7 Số điểm: 3.5	Số câu:8 Số điểm: 4.0	Số câu: 2 Số điểm: 1.0	*Số câu: 20* *Số điểm: 10*

Đề thi cuối kì 1 Toán 9 – Đề 3

Đề thi học kì 1 Toán 9

PHÒNG GD&ĐT ………….

TRƯỜNG THCS ……..

ĐỀ KIỂM TRA CUỐI HỌC KỲ I

NĂM HỌC: 2022– 2023

MÔN TOÁN – LỚP 9

Thời gian làm bài 90 phút (không kể thời gian phát đề)

Xem thêm: Tìm m để phương trình có nghiệm nguyên

Câu 1 (2 điểm):

1) Tính giá trị của biểu thức

$a) sqrt{12}-sqrt{27}+frac{1}{2} sqrt{48}$

$b) (sqrt{2}-1) sqrt{3+2 sqrt{2}}$

2) Giải hệ phương trình $left{begin{array}{l}x+3 y=4 3 x-2 y=1end{array}right.$

3) Tìm a để phương trình $mathrm{ax}+2 mathrm{y}=5$ nhân cấp số (3 ; 1) làm nghiệm

Câu 2 (2 điểm): Cho hàm số: $mathrm{y}=(mathrm{m}+1) mathrm{x}-2 mathrm{~m} (d)$

a) Xác định m để hàm số trên là hàm số nghịch biến?

b) Vẽ đồ thị hàm số trên khi m=1

c) Xác định m để đồ thị hàm số trên song song với đường thẳng y=3 x+6 ?

Câu 3 (2 điểm): Cho biểu thức $mathrm{A}=left(frac{sqrt{x}}{x-4}-frac{1}{sqrt{x}+2}right): frac{sqrt{x}-2}{x-4}$

a) Tìm ĐKXÐ và rút gọn biểu thức A

b) Tìm giá trị của x để $mathrm{A}<mathrm{O}$

c) Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên

Câu 4 (3.5 điểm):Cho tam giác ABC vuông tại A (AB > AC), có đường cao AH.

1. Cho AB = 4cm; AC = 3cm. Tính độ dài các đoạn thẳng BC, AH.

2. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai D.

a) Chứng minh BD là tiếp tuyến của đường tròn (C).

b) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA, BD thứ tự tại E, F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB, BD lần lượt tại P, Q. Chứng minh: $2 sqrt{P E cdot Q F}=E F$

Câu 5 (0.5 điểm): Giải phương trình:

$x^{2}+4 x+7=(x+4) sqrt{x^{2}+7}$

Đáp án đề thi HK1 Toán 9

Câu	Nội dung đáp án	Điểm
1 (2 điểm)	a) = $sqrt{12}-sqrt{27}+frac{1}{2} sqrt{48}$ $=2 sqrt{3}-3 sqrt{3}+frac{1}{2} cdot 4 sqrt{3}$ $=(2-3+2) sqrt{3} =sqrt{3}$	0.5đ
	b)) = $(sqrt{2}-1) sqrt{3+2 sqrt{2}}=(sqrt{2}-1) sqrt{2+2 sqrt{2}+1}=(sqrt{2}-1) sqrt{(sqrt{2}+1)^{2}}$ = $=(sqrt{2}-1)(sqrt{2}+1)=2-1=1$	0.5đ
	2) $left{begin{array}{l}x+3 y=4 3 x-2 y=1end{array} Leftrightarrowleft{begin{array}{l}3 x+9 y=12 3 x-2 y=1end{array} Leftrightarrowleft{begin{array}{l}11 y=11 3 x-2 y=1end{array} Leftrightarrowleft{begin{array}{l}y=1 x=1end{array}right.right.right.right.$	0.5đ
	3) Phương trình ax +2y =5 nhận cặp số (3;1) làm nghiệm khi a.3+2.1=5. 3a=3 suy ra a=1	0.25đ 0,25đ
2 (2 điểm)	a) y = (m+1)x -2m (d) Hàm số trên nghịch biếnkhi m+1<0 → m<-1	0.75đ
	b) Với m=1 thì hàm số có dạng: y=2x – 2(d1) HS trình bày đầy đủ các bước và vẽ đúng	0.75đ
	c) Đồ thị hàm số (d) song song với đường thẳng y=3x+6 . Vậy m=2	0.5đ

…………….

Ma trận đề thi HK1 Toán 9

Cấp độ Chủ đề	Nhận biết	Thông hiểu	Vận dụng		Cộng
			*Cấp độ thấp*	*Cấp độ cao*
	TL	TL	TL	TL
1.Căn thức bậc hai	– Xác định điều kiện có nghĩa của căn bậc hai.	-Hiểu được hằng đẳng thức để rút gọn biểu thức	Vận dụng các phép biến đổi đơn giản để rút gọn biểu thức, tính giá trị biểu thức	Vận dụng các phép biến đổi để rút gọn biểu thức phức tạp, giải phương trình vô tỷ
	Số câu:2 Số điểm:1	Số câu:2 Số điểm:1	Số câu:2 Số điểm: 1.	Số câu:1 Số điểm:0,5	*Số câu: 7* *Số điểm:3.5*
2.Hàm số bậc nhất	Nhận biết được hàm số đồng biến, nghich biến	Hiểu được hai đường thẳng song song,.. Vẽ được đồ thị hàm số	Tìm được giao điểm đồ thị của hai hàm số bậc nhất
	Số câu:2 Số điểm:1	Số câu:2 Số điểm:1	Số câu:2 Số điểm:1		*Số câu: 6* *Số điểm: 3*
3.Hệ thức lượng trong tam giác vuông.		Hiểu được các hệ thức áp dụng vào tam giác vuông	Vận dụng các hệ thức lượng trong tam giác vuông để giải toán
		Số câu:1 Số điểm:0.5	Số câu:1 Số điểm:0.5		*Số câu: 2* *Số điểm:* *1.0*
4. Đường tròn	Nhận biết được đường tròn	Hiểu được tính chất đường tròn, hai tiếp tuyến cắt nhau để chứng minh	Vận dụng khái niệm đường tròn và các tính chất đường tròn, hai tiếp tuyến cắt nhau của đường tròn để chứng minh
	Số câu:1 Số điểm: 05	Số câu:1 Sốđiểm:0.5	Số câu:2 Số điểm 1	Số câu:1 Số điểm:0.5	*Số câu: 5* *Số điểm:3*
*Tổng*	Số câu:4 Số điểm: 2.0	Số câu: 7 Số điểm: 3.5	Số câu:8 Số điểm: 4.0	Số câu: 2 Số điểm: 1.0	*Số câu: 20* *Số điểm: 10*

…………….

Mời các bạn tải File tài liệu để xem thêm nội dung 4 đề thi học kì 1 Toán 9 năm 2022

[ad_2]

Đăng bởi: THPT An Giang

Chuyên mục: Học Tập

Bộ đề thi học kì 1 Toán 9 năm 2022 – 2023 có đáp án

Đề thi học kì 1 Toán 9 – Đề 1

Đề thi học kì 1 Toán 9

Đáp án đề thi học kì 1 Toán 9

Ma trận đề thi học kì 1 Toán 9

Đề thi cuối kì 1 Toán 9 – Đề 2

Đề thi học kì 1 Toán 9

Ma trận đề thi học kì 1 Toán 9

Đề thi cuối kì 1 Toán 9 – Đề 3

Đề thi học kì 1 Toán 9

Đáp án đề thi HK1 Toán 9

Ma trận đề thi HK1 Toán 9

Toán 10 Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài tập phân tích đa thức thành nhân tử

Viết một bình luận Hủy