Nội dung đang xem: Toán 10 Bài 3: Tích của một số với một vectơ
Giải Toán 10 Bài 3: Tích của một số với một vectơ sách Chân trời sáng tạo giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo để giải các bài tập phần luyện tập, vận dụng và bài tập trang 97 tập 1 được nhanh chóng và dễ dàng hơn.
Giải Toán 10 trang 97 Tập 1 sách Chân trời sáng tạo giúp các em luyện tập, giải các bài tập về Tích của một số với một vectơ. Giải bài tập Toán 10 Tích của một số với một vectơ được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết Giải Toán lớp 10: Tích của một số với một vectơ trang 97, mời các bạn cùng tải tại đây.
Giải Toán 10 trang 97 Chân trời sáng tạo – Tập 1
Bài 1 trang 97
Cho hình bình hành ABCD D có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:
Gợi ý đáp án
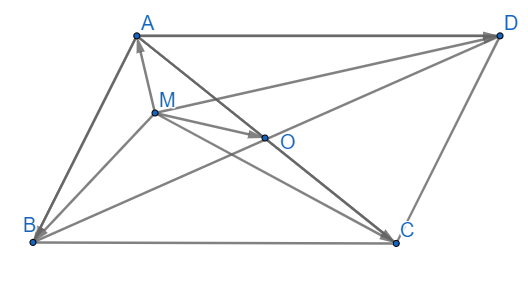
a)
(luôn đúng)
(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)
b) ABCD là hình bình hành nên ta có
Suy ra (đpcm)
Bài 2 trang 97
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng
Gợi ý đáp án
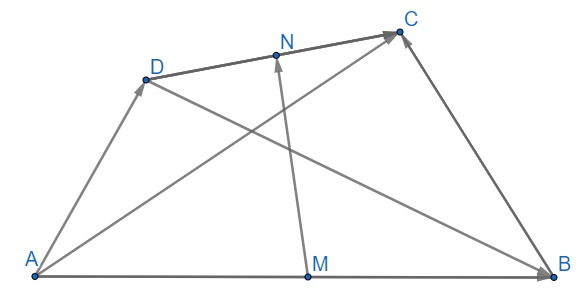
(đpcm)
b)
Mặt khác ta có:
Suy ra
Bài 3 trang 97
Cho hai điểm phân biệt A và B. Xác định điểm M sao cho
Gợi ý đáp án
ngược hướng
Suy ra M nằm giữa AB sao cho
Bài 4 trang 97
Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng
Gợi ý đáp án
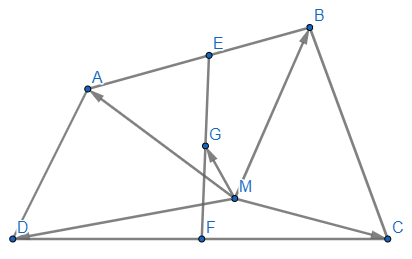
(đpcm)
Bài 5 trang 97
Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc \overrightarrow b của máy bay B theo vectơ vận tốc của máy bay A
Gợi ý đáp án
vectơ là vectơ vận tốc của máy bay A và máy bay b.
Do đó lần lượt là độ lớn của vectơ vận tốc tương ứng.
Ta có:
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó
Bài 6 trang 97
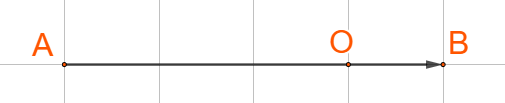
Cho 2 điểm phân biệt A và B
a) Xác định điểm O sao cho
b) Chứng minh rằng với mọi điểm M, ta có
Gợi ý đáp án
Vậy O thuộc đoạn AB sao cho
b) Ta có:
Bài 7 trang 97
Cho tam giác ABC
a) Xác định các điểm M, N, P thỏa mãn:
b) Biểu thị mỗi vectơ theo hai vectơ
c) Chứng minh ba điểm M, N, P thẳng hàng
Gợi ý đáp án
a) Ta có:
+) và
cùng hướng; tỉ số độ dài
nằm ngoài đoạn thẳng BC sao cho
thuộc đoạn thẳng AB và
là trung điểm của CA
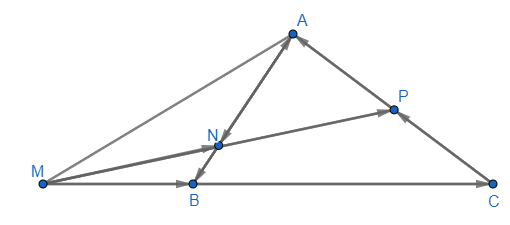
c) Ta có:
Vậy M,N,P thẳng hàng
Lý thuyết Tích của một số với một vectơ
[ad_2]
Đăng bởi: THPT An Giang
Chuyên mục: Học Tập
