Toán Lớp 7

Toán 7 Luyện tập chung trang 74

Photo of author

By THPT An Giang

[ad_1]

Nội dung đang xem: Toán 7 Luyện tập chung trang 74

Giải Toán 7 Luyện tập chung giúp các em học sinh lớp 7 tham khảo phương pháp giải, hướng dẫn giải chi tiết các bài tập trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống trang 74.

Qua đó, các em sẽ biết cách chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh, góc – cạnh – góc. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Luyện tập chung Chương IV: Tam giác bằng nhau trong SGK Toán 7 Tập 1 Kết nối tri thức với cuộc sống. Chi tiết mời thầy cô và các em cùng theo dõi:

Giải Toán 7 bài Luyện tập chung trang 74 Kết nối tri thức với cuộc sống

Giải Toán 7 Kết nối tri thức với cuộc sống trang 74 tập 1

Bài 4.16

Cho hai tam giác ABC và DEF thoả mãn AB = DE,AC = DF,widehat {BAC} = widehat {EDF} = {60^circ },BC = 6;{rm{cm}},widehat {ABC} = {45^circ }. Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.

Phương pháp giải:

Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.

Từ đó suy ra các cặp cạnh và các cặp góc tương ứng bằng nhau.

Gợi ý đáp án:

Bài 4.16

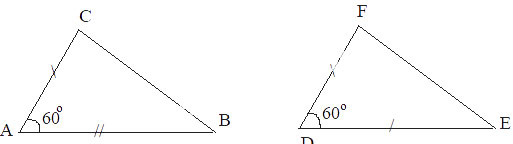
Xét hai tam giác ABC và DEF có:

Xem thêm:  Số hữu tỉ: Lý thuyết và Bài tập về số hữu tỉ

begin{array}{l}AB = DE\AC = DF\widehat {BAC} = widehat {EDF} = {60^circ }end{array}

Rightarrow Delta ABC = Delta DEF(c.g.c)

Do đó:

EF = BC = 6cm

widehat {DEF} = widehat {ABC} = {45^o}

begin{array}{l}widehat {BAC} + widehat {ABC} + widehat {ACB} = {180^o}\ Rightarrow {60^o} + {45^o} + widehat {ACB} = {180^o}\ Rightarrow widehat {ACB} = {75^o}end{array}

Rightarrow widehat {EFD} = widehat {ACB} = {75^o}

Bài 4.17

Cho hai tam giác ABC và DEF thoả mãn AB = DE, widehat {ABC} = widehat {DEF} = {70^circ },widehat {BAC} = widehat {EDF} = {60^circ },AC = 6;{rm{cm}}.

Tính độ dài cạnh DF.

Phương pháp giải:

Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.

Gợi ý đáp án:

Xét hai tam giác ABC và DEF có:

begin{array}{l}widehat {ABC} = widehat {DEF} (= {70^circ })\AB = DE\widehat {BAC} = widehat {EDF} (= {60^circ })end{array}

Rightarrow Delta ABC{rm{ = }}Delta DEF(g.c.g)

Rightarrow DF = AC (2 cạnh tương ứng)

Mà AC = 6 cm

Rightarrow DF = 6cm

Bài 4.18

Cho Hình 4.44, biết EC = ED và widehat {AEC} = widehat {AED}. Chứng minh rằng:

begin{array}{*{20}{l}}{{rm{ a) }}Delta AEC = Delta AED;}&{{rm{ b) }}Delta ABC = Delta ABD.}end{array}

Hình 4.44

Phương pháp giải:

Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.

Gợi ý đáp án:

a) Xét hai tam giác AEC và AED có

EC = ED

widehat {CEA} = widehat {DEA}

AE chung

Rightarrow Delta AEC{rm{ = }}Delta AED(c.g.c)

b) Do Delta AEC{rm{ = }}Delta AED nên widehat {CAE} = widehat {DAE} (2 góc tương ứng) và AC=AD (2 cạnh tương ứng).

Xét Delta ABC và Delta ABD có:

AB chung

widehat {CAE} = widehat {DAE}

AC=AD

Rightarrow Delta ABC = Delta ABD(c.g.c)

Bài 4.19

Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho widehat {CAO} = widehat {CBO}.

a) Chứng minh rằng Delta OAC = Delta OBC.

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng Delta MAC = Delta MBC.

Phương pháp giải:

a) Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.

b) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.

Gợi ý đáp án:

Bài 4.19

a) Xét Delta OAC và Delta OBC có:

widehat {AOC} = widehat {AOB}(Oz là phân giác góc xOy)

OC chung

widehat {CAO} = widehat {CBO}

Rightarrow Delta OAC = Delta OBC(g.c.g)

b) Do Delta OAC = Delta OBC nên AC=BC (2 cạnh tương ứng)

Vì widehat {ACO} và widehat {ACM} kề bù

widehat {BCO} và widehat {BCM} kề bù

Mà widehat {ACO} = widehat {BCO} nên widehat {ACM} = widehat {BCM}

Xét Delta MAC và Delta MBC có:

AC=BC

widehat {ACM} = widehat {BCM}

CM chung

Rightarrow Delta MAC = Delta MBC(c.g.c)

[ad_2]

Đăng bởi: THPT An Giang

Chuyên mục: Học Tập

Bài tập phân tích đa thức thành nhân tử

Toán 6 Bài tập cuối chương II – Kết nối tri thức với cuộc sống

Viết một bình luận