Nội dung đang xem: Giải Toán 8 Bài 3: Hình thang cân
Giải bài tập SGK Toán 8 Bài 3: Hình thang cân giúp các em học sinh lớp 8 tổng hợp toàn bộ kiến thức lý thuyết quan trọng, nhanh chóng trả lời câu hỏi trong nội dung bài học, cùng 9 bài tập của Bài 3 Chương I Hình học 8 tập 1 trang 74, 75.
Với lời giải chi tiết, trình bày khoa học sẽ giúp các em nhanh chóng giải toàn bộ bài tập của Bài 3 Hình học trong SGK Toán 8. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
Trả lời câu hỏi trang 72, 74 SGK Toán 8 tập 1
Câu hỏi 1
Hình thang ABCD (AB // CD) trên hình 23 có gì đặc biệt?
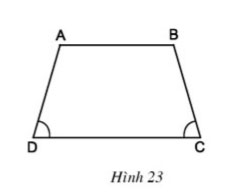
Gợi ý đáp án:
Hình thang ABCD trên hình 23 có hai góc kề cạnh đáy lớn bằng nhau
Câu hỏi 2
Cho hình 24.
a) Tìm các hình thang cân.
b) Tính các góc còn lại của mỗi hình thang cân đó.
c) Có nhận xét gì về hai góc đối của hình thang cân?
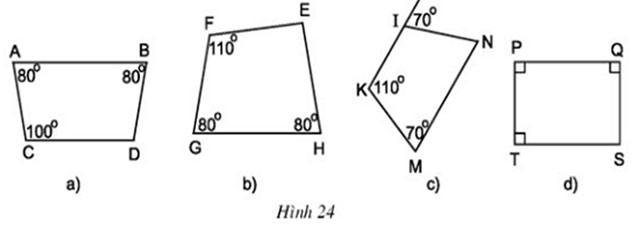
Gợi ý đáp án:
a) Các hình thang cân là: ABDC, IKMN, PQST
b) Áp dụng định lí tổng các góc của một tứ giác bằng 3600
⇒ góc
Góc N = 70o(so le trong với góc 70o)
Góc
c) Hai góc đối của hình thang cân bù nhau
Câu hỏi 3
Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc C và D của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.
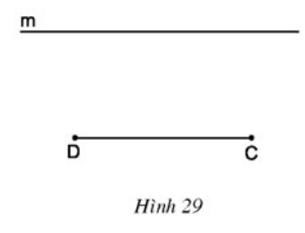
Gợi ý đáp án:
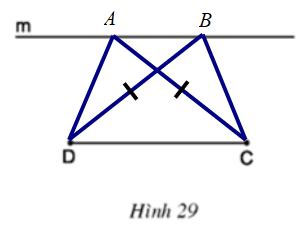
Hai góc C và D bằng nhau
⇒ Hình thang có hai đường chéo bằng nhau là hình thang cân
Giải bài tập toán 8 trang 74, 75 tập 1
Bài 11
Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (hình 30, độ dài của cạnh ô vuông là 1cm)
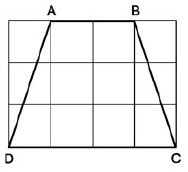
Hình 30
Gợi ý đáp án:
Với độ dài cạnh ô vuông là 1cm thì: AB = 2 cm và DC = 4 cm
Kẻ , ta có AH = 3 cm
Áp dụng định lí Pi-ta-go trong tam giác vuông AHD, ta có:
ABCD là hình thang cân nên
Bài 12
Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
Gợi ý đáp án:
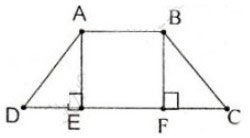
Xét hai tam giác vuông AED và BFC, ta có:
AD = BC (ABCD là hình thang cân)
(ABCD là hình thang cân)
Nên (cạnh huyền – góc nhọn)
Suy ra DE = CF (đpcm)
Bài 13
Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED
Gợi ý đáp án:
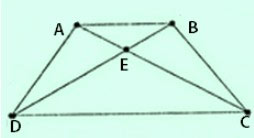
Xét hai tam giác ADC và BCD có:
AD = BC (ABCD là hình thang cân)
AC = BD (hai đường chéo của hình thang cân)
DC chung
Nên
Suy ra
Do đó cân tại E
Suy ra EC = ED
Mặt khác AC = BD nên EA = EB
Bài 14
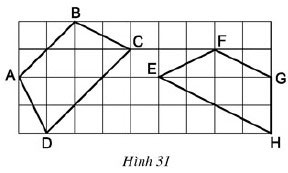
Đố. Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), Tứ giác nào là hình thang cân? Vì sao?
Gợi ý đáp án:
Quan sát hình 31, dựa vào tính chất hai cạnh bên của hình thang, ta thấy:
Tứ giác ABCD có AD = BC nên ABCD là hình thang cân.
Tứ giác EHGF có nên EHGF không phải là hình thang cân.
Bài 15
Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE
a) Chứng mình rằng BDEC là hình thang cân
b) Tính các góc của hình thang đó, biết rằng
Gợi ý đáp án:
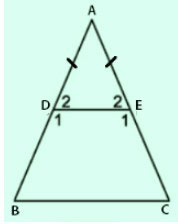
a) Ta có:
AD = AE nên cân tại A
Trong tam giác ADE có:
Tương tự trong tam giác ABC ta cũng có:
Từ (1) và (2) suy ra
Do đó DE // BC ⇒ BDEC là hình thang.
Mặt khác (ABC là tam giác cân)
Nên BDEC là hình thang cân.
b) Với , ta có:
Giải bài tập toán 8 trang 75 tập 1: Luyện tập
Bài 15
Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Gợi ý đáp án:
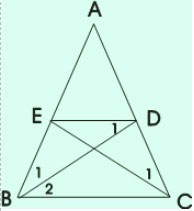
Ta có:
(BD là phân giác)
(CE là phân giác)
Mà (tam giác ABC cân tại A)
Nên
Xét hai tam giác ADB và AEC có:
chung
AB = AC (tam giác ABC cân tại A)
(chứng minh trên)
Do đó
Suy ra AD = AE
Nên tam giác ADE cân tại A
Ta có:
(tam giác ADE cân tại A)
(tam giác ABC cân tại A)
Suy ra
Nên ED // BC
Do đó: tứ giác BEDC là hình thang
Hình thang BEDC có nên BEDC là hình thang cân.
Ta có (so le trong)
Mà (chứng minh trên)
Nên
Do đó tam giác BED cân tại E
Suy ra EB = ED
Vậy hình thang BEDC là hình thang cân có đáy nhỏ ED bằng cạnh bên EB.
Bài 17
Hình thang ABCD (AB//CD) có . Chứng minh rằng ABCD là hình thang cân.
Gợi ý đáp án:
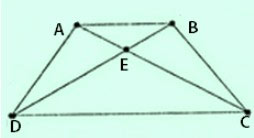
Ta có
nên tam giác DEC cân tại E
Suy ra ED = EC (1)
Ta lại có:
Mà
Nên
Do đó tam giác AEB cân tại A ⇒ EA = EB (2)
Từ (1) và (2) suy ra: AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên ABCD là hình thang cân.
Bài 18
Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang ABCD (AB//CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng minh rằng:
a) là tam giác cân
b) .
c) Hình thang ABCD là hình thang cân
Gợi ý đáp án:
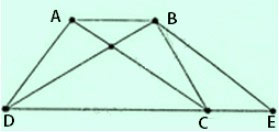
a) Ta có
⇒ AC = BE
Ta lại có: AC = BD (gt) ⇒ BE = BD
Do đó tam giác BDE cân tại B.
b) Ta có (hai góc đồng vị)
Ta lại có:
(tam giác BDE cân tại B)
Xét hai tam giác ACD và BDC có:
Cạnh DC chung
(chứng minh trên)
AD = BD (gt)
Nên
c) Hình thang ABCD có:
Nên hình thang ABCD là hình thang cân.
Bài 19
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn điểm của hình thang cân.
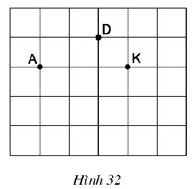
Gợi ý đáp án:
Nếu cạnh của mỗi ô vuông là 1 đơn vị thì:
Ta có: AK = 3 nên ta phải chọn M sao cho AM//DK và DM = 3. Khi đó ta được hình thang cân ADKM như hình dưới đây.
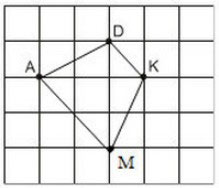
Lý thuyết bài 3: Hình thang cân
1. Định nghĩa
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
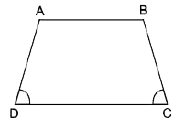
Tứ giác ABCD là hình thang cân (đáy AB; CD)
và
2. Tính chất
Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.

Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.
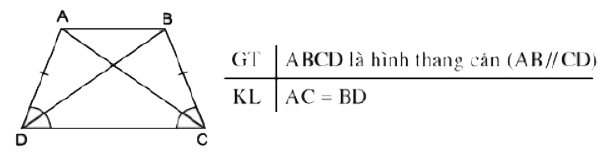
Định lí 3: Hình thang có hai đường chéo bằng nhau là hình thang cân.
3. Dấu hiệu nhận biết hình thang cân
Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Hình thang có hai đường chéo bằng nhau là hình thang cân.
[ad_2]
Đăng bởi: THPT An Giang
Chuyên mục: Học Tập
