Nội dung đang xem: Giải Toán 9 Bài 2: Tỉ số lượng giác của góc nhọn
Giải Toán 9 bài 2: Tỉ số lượng giác của góc nhọn giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập phần câu hỏi và bài tập được nhanh chóng và dễ dàng hơn.
Giải Toán 9 trang 76, 77 giúp các em hiểu được thế nào là Tỉ số lượng giác của góc nhọn, các dạng toán thường gặp. Giải Toán 9 bài 2 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết Giải Toán lớp 9 Bài 2: Tỉ số lượng giác của góc nhọn, mời các bạn cùng tải tại đây.
Lý thuyết Tỉ số lượng giác của góc nhọn
1. Định nghĩa Tỉ số lượng giác của góc nhọn
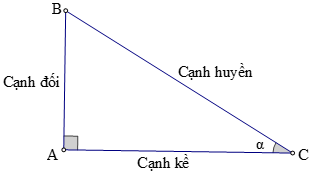
2. Các dạng toán thường gặp
Dạng 1: Tính Tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp:
Sử dụng các Tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Dạng 2: So sánh các tỉ số lượng giác giữa các góc
Phương pháp:
Bước 1 : Đưa các tỉ số lượng giác về cùng loại (sử dụng tính chất “Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia”)
Bước 2: Với góc nhọn ta có:
![]()
![]()
Dạng 3: Rút gọn, tính giá trị biểu thức lượng giác
Phương pháp:
Ta thường sử dụng các kiến thức
+ Nếu là một góc nhọn bất kỳ thì
![]()
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Giải bài tập toán 9 trang 76, 77 tập 1
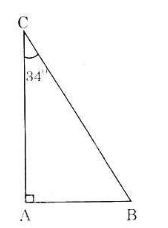
Bài 10 (trang 76 SGK Toán 9 Tập 1)
Vẽ một tam giác vuông có một góc nhọn 34o rồi viết các tỉ số lượng giác của góc 34o.
Gợi ý đáp án
ΔABC vuông tại A có góc C = 34o.
Khi đó:
Tỉ số lượng giác của góc là:
Bài 11 (trang 76 SGK Toán 9 Tập 1)
Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2m. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.
Gợi ý đáp án
Xét vuông tại C, áp dụng định lí Pytago, ta có:
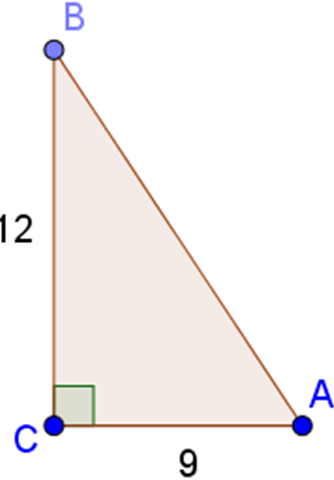
Vì vuông tại C nên góc B và A là hai góc phụ nhau. Do vậy, ta có:
Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tan góc này bằng cotan góc kia!
Bài 12 (trang 76 SGK Toán 9 Tập 1)
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45o: sin60o, cos75o, sin52o30′, cotg82o, tg80o
Gợi ý đáp án
(Áp dụng tính chất lượng giác của hai góc phụ nhau.)
Vì 60o + 30o = 90o nên sin60o = cos30o
Vì 75o + 15o = 90o nên cos75o = sin15o
Vì 52o30′ + 37o30′ = 90o nên sin 52o30’= cos37o30′
Vì 82o + 8o = 90o nên cotg82o = tg8o
Vì 80o + 10o = 90o nên tg80o = cotg10o
Giải bài tập toán 9 trang 77 tập 1: Luyện tập
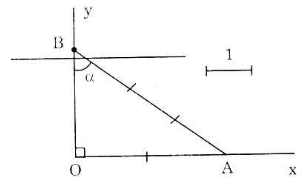
Bài 13 (trang 77 SGK Toán 9 Tập 1)
Gợi ý đáp án
Dựng góc nhọn , biết:
Ta thực hiện các bước sau:
– Dựng góc vuông xOy. Lấy một đoạn thẳng làm đơn vị.
– Trên tia Ox lấy điểm A bất kỳ sao cho: OA=2.
– Dùng compa dựng cung tròn tâm A, bán kính 3. Cung tròn này cắt Oy tại điểm B.
– Nối A với B. Góc OBA là góc cần dựng.
Thật vậy, xét vuông tại O, theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
b.
Ta có:
– Dựng góc vuông xOy. Lấy một đoạn thẳng làm đơn vị.
– Trên tia Ox lấy điểm A bất kỳ sao cho OA=3.
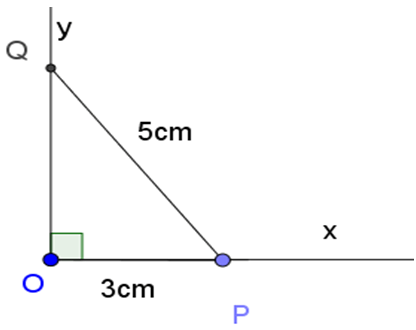
– Dùng compa dựng cung tròn tâm A bán kính 5. Cung tròn này cắt tia Oy tại B.
– Nối A với B. Góc là góc cần dựng.
Thật vậy, Xét vuông tại O, theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
– Dựng góc vuông xOy. Lấy một đoạn thẳng làm đơn vị.
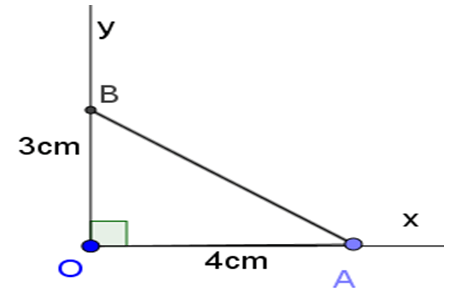
– Trên tia Ox lấy điểm A sao cho OA=4.
Trên tia Oy lấy điểm B sao cho OB=3.
– Nối A với B. Góc là góc cần dựng.
Thật vậy, xét vuông tại O, theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
– Dựng góc vuông xOy. Lấy một đoạn thẳng làm đơn vị.
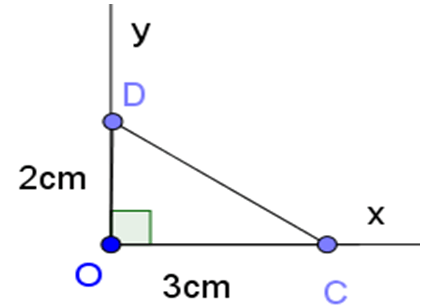
– Trên tia Ox lấy điểm A sao cho OA=3.
Trên tia Oy lấy điểm B sao cho OB=2.
– Nối A với B. Góc là góc cần dựng.
Thật vậy, xét vuông tại O, theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
Bài 14 (trang 77 SGK Toán 9 Tập 1)
Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn tùy ý, ta có:
a)
Gợi ý đáp án
Xét vuông tại A, có
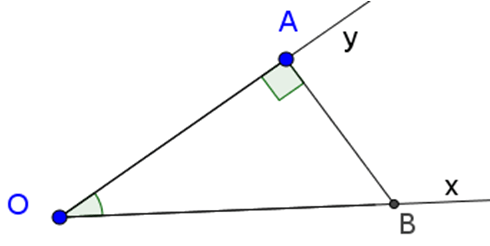
+) vuông tại A, theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
* Chứng minh
(Trong đó VT là vế trái của đẳng thức; VP là vế phải của đẳng thức)
* Chứng minh
* Chứng minh
Ta có:
b) vuông tại A, áp dụng định lí Pytago, ta được:
Xét
Thay (1) vào (2) ta được:
Như vậy (điều phải chứng minh)
Nhận xét: Ba hệ thức:
và
là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.
Bài 15 (trang 77 SGK Toán 9 Tập 1)
Cho tam giác ABC vuông tại A. Biết cosB=0,8, hãy tính các tỉ số lượng giác của góc C.
Gợi ý: Sử dụng bài tập 14.
Gợi ý đáp án
Xét tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
![]()
Vì hai góc B và C phụ nhau
Áp dụng công thức bài 14, ta có:
Lại có:
Nhận xét: Nếu biết thì ta có thể tính được ba tỷ số lượng giác còn lại.
Bài 16 (trang 77 SGK Toán 9 Tập 1)
Cho tam giác vuông có một góc 60o và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60o.
Gợi ý đáp án
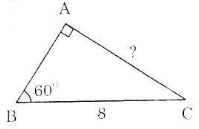
Bài 17 (trang 77 SGK Toán 9 Tập 1)
Tìm x trong hình 23.
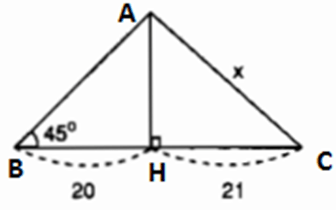
Gợi ý đáp án
Kí hiệu như hình trên.
Ta có tam giác ABH là vuông cân (vì ∠B = 45o) nên AH = 20.
Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841
=> x = √841 = 29
[ad_2]
Đăng bởi: THPT An Giang
Chuyên mục: Học Tập
